Kwartierstaat

Inleiding

Kwartierverlies

Kwartierherhaling

Inleiding

De basis voor deze genealogie is de kwartierstaat van mijn dochter Marit Terweij. In een kwartierstaat zijn de directe voorouders van een individu opgenomen. Schematisch is een kwartierstaat weer te geven als een omgekeerde driehoek:

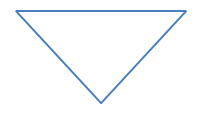
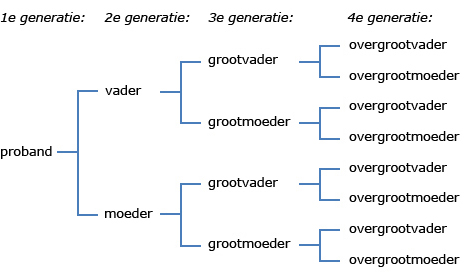
Een kwartierstaat begint onderaan met een individu, een man of een vrouw: de proband. Dit is de eerste generatie. Dan volgt de tweede generatie met de twee ouders van de proband. Daarna komt de derde generatie met de vier grootouders. Dan de vierde generatie met de acht overgrootouders. Enzovoort. Per generatie verdubbelt het aantal voorouders. Partners uit eerdere en latere huwelijken van directe voorouders komen in de kwartierstaat niet voor, want dat zijn geen directe voorouders van de proband, het is geen familie in rechte lijn. In paren-
teelstaten (zie hierna) zijn deze partners wel opgenomen, want het is wel familie in zijlijn.

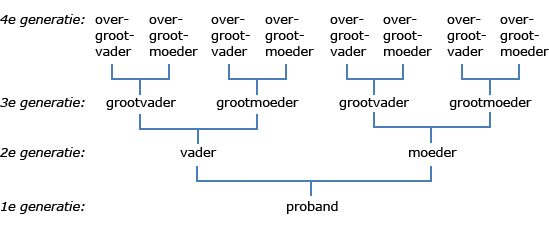
In genealogische softwareprogramma's wordt de kwartierstaat vaak een kwart slag gedraaid. De lengte van de tekstvelden is dan beter te variëren.

Kwartierverlies

Er komt onvermijdelijk een moment dat er geen bronnen meer zijn te vinden, er is dan sprake van kwartierverlies:
• De voorouder is een bastaardkind waarvan de vader onbekend is of een vondeling, dan is ook de moeder onbekend.
• De archieven zijn verloren gegaan door natuurgeweld, oorlog, brand, overstroming, muizen, schimmels, enz.
• Vóór enig moment werden er gewoonweg geen archieven bijgehouden.
Veel auteurs beperken kwartierverlies tot ongehuwde moeders waarbij de vader niet te achterhalen is, of vondelingen en pleegkinderen; zij sluiten het algemeen ontbreken van bronnen uit (zie bijvoorbeeld R.F Vulsma, Gensdatapro, Persoonsnummering). Ik ben het daarmee niet eens en sta daarin niet alleen, zie ook Wikipedia.
Eigenlijk is de term kwartierverlies niet erg gelukkig: de kwartieren zijn er wel, maar we kennen ze niet of nog niet. Om niet verzeild te raken in de filosofische aspecten van bestaan en werkelijkheid (Sein und Zeit), hier een voorbeeld uit de praktijk van mijn eigen genealogie.

Toen ik indertijd de computer ging toepassen in mijn genealogisch onderzoek, was ik niet erg te spreken over de beschikbare computerprogramma's (en nog steeds niet). Ik heb toen een eigen toepassing gemaakt in MS Access, het relationele databaseprogramma van Microsoft. Een bruikbaar programma, maar zeker geen intelligente programmeeromgeving.
Voor ieder individu moest ruimte – lees: een vakje – voorbereid zijn, ook voor de individuen waarvan nog geen naam of gegevens bekend waren. Bij het genereren van de grafische overzichten werden vervolgens de niet gebruikte vakjes verborgen. Dit was natuurlijk alleen mogelijk door de database te beperken: maximaal 16 generaties, 15 kinderen per gezin en drie partners per individu. Bij ruimtegebrek liet ik doodgeboren of jonggestorven kinderen en kinderloze huwelijken weg en nam deze op in een voetnoot.
Het werd pas echt een probleem toen ik aansluiting vond bij een genealogie die terugging tot het jaar 1330. Voor zes extra generaties met zestien namen zou ik 4.128.762 vakjes extra moeten reserveren, om deze vervolgens weer te verbergen op 16 na. Toen werd het tijd voor een echt genealogieprogramma: RootsMagic. Nog steeds koester ik dezelfde bezwaren, ook bij dit relatief goede programma, maar ik kan er in ieder geval GEDCOM-bestanden mee maken om deze website te bouwen.

Kwartierherhaling

Net als kwartierverlies is ook kwartierherhaling onvermijdelijk. Er treedt kwartierherhaling op als paren in de kwartierstaat dezelfde voorouders hebben. In de kwartierstaat van mijn dochter Marit komt dit tot nu toe vier keer voor.
a. [650] Claas Willemsz. Hoogeland en [651] Susanna Christiaans krijgen twee dochters: [325] Antje en [327] Maartje. Antje krijgt een zoon: [162] Steven Jetses Bakker en Maartje krijgt een dochter: [163] Trijntje Willems Snel. Zij zijn neef en nicht en trouwen, dat was in die tijd geen enkel probleem.
b. Vergelijkbaar is de situatie bij [2034] Dirk van Slot. Hij heeft twee dochters: [1017] Catharina en [1019] Annetje. De zoon van Catharina: [508] Dirk Jacobs Immerzeel en de dochter van Annetje: [509] Ariaantje de Groot zijn neef en nicht, ook zij trouwen.
c. Als een oom het met zijn nichtje deed, was dat wél een probleem. [192] Dieterich Hermann Redeker en [193] Anna Ilse Honeiken krijgen een zoon en een dochter: [96] Johann Diedrich Rädecker (eigenlijk 195.2) en [195] Anne Sophie Engel Redecker. Anne Sofie Engel krijgt een dochter: [97] Sophia Marie Hansing. Sophia Marie en haar oom Johann Diedrich hebben een relatie waaruit in onecht de zoon [46] Heinrich Wilhelm Rädecker geboren wordt, stamvader van alle Rädeckers in Nederland.
d. De gemeenschappelijke voorouder van [458] Johannes Dorrepaal en [459] Maartje Nijgh is [7332] Leendert Nijg. Daar zitten dan wel vier generaties tussen, ongeveer 130 jaar, waarschijnlijk was men toen niet op de hoogte van deze familierelatie.

Kwartierherhaling is onvermijdelijk. Mijn dochter is geboren aan het eind van de 20ste eeuw. Als we uitgaan van drie generaties per eeuw, dan zouden rond het jaar 1000 meer dan 1 miljard mensen moeten hebben geleefd, die duizend jaar later tot de conceptie van Marit hebben geleid. Bij vier generaties per eeuw, wat ook geen vreemde veronderstelling is, kom je nog veel hoger uit.
Echter, de omvang van de wereldbevolking rond het jaar 1000 wordt geschat op 254 tot 345 miljoen (US Census Bureau, Wikipedia). Het grondgebied van het huidige Nederland, de noordelijke Nederlanden, bestond in die tijd voornamelijk uit moerassen en wadden, met bossen op de hoger gelegen zandgronden in het oosten en op de strandwallen in het westen. Er woonden toen niet meer dan 200.000 mensen (Paolo Malanima, Energy and population in Europe, 2010, blz. 5). De bevolking concentreerde zich in de zuidelijke Nederlanden (600.000 mensen), ruwweg het huidige België, daar bloeide het culturele en economische leven.

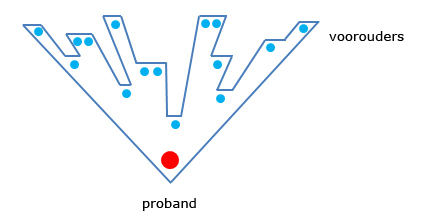
Door kwartierverlies en kwartierherhaling zal de omgekeerde driehoek in de schematische voorstelling een wat rafelige bovenkant hebben: